Систему неоднородных уравнений
запишем в матричном виде 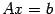 , где
матрица
, где
матрица 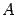 имеет размеры
имеет размеры 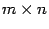 .
.
Предложение 15.4 Пусть 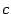 и
и 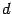 --
решения неоднородной системы
--
решения неоднородной системы 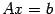 . Тогда их
разность
. Тогда их
разность 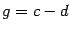 является
решением однородной системы с той же матрицей, то есть решением системы
является
решением однородной системы с той же матрицей, то есть решением системы 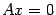 .
.
Доказательство. По условию 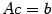 и
и 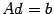 . Тогда
Так как
. Тогда
Так как 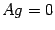 , то
, то 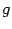 -- решение однородной системы.
-- решение однородной системы.
Предложение 15.5 Пусть 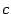 -- решение неоднородной системы
-- решение неоднородной системы 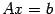 ,
, 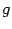 -- любое решение однородной системы
-- любое решение однородной системы 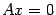 . Тогда
. Тогда 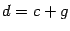 --
решение неоднородной системы.
--
решение неоднородной системы.
Доказательство предоставляется читателю.
Определение 15.7 Пусть
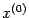
-- некоторое решение неоднородной
системы линейных уравнений
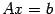
,
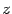
-- общее решение однородной системы
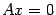
. Тогда выражение
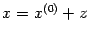
называется
общим решением неоднородной системы.
Учитывая запись общего решения однородной системы через фундаментальную
систему ее решений 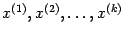 ,
получаем для общего решения неоднородной системы формулу
,
получаем для общего решения неоднородной системы формулу
Из двух последних предложений следует, что любое решение неоднородной системы
может быть получено из общего решения при некоторых числовых значениях
коэффициентов 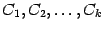 .
.
Теорема 15.4 Система
линейных уравнений 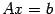 может
иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.
может
иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.
Доказательство. Пусть система имеет
решение 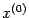 . Если
однородная система
. Если
однородная система 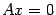 имеет
только одно решение, то из формулы общего решения будет следовать, что
имеет
только одно решение, то из формулы общего решения будет следовать, что 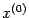 -- единственное решение
неоднородной системы. Если однородная система имеет хотя бы одно ненулевое
решение, то ее фундаментальная система решений будет состоять не менее, чем из
одного решения. В формуле общего решения неоднородной системы будет произвольный
коэффициент
-- единственное решение
неоднородной системы. Если однородная система имеет хотя бы одно ненулевое
решение, то ее фундаментальная система решений будет состоять не менее, чем из
одного решения. В формуле общего решения неоднородной системы будет произвольный
коэффициент 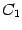 , и при
различных его значениях мы будем получать различные решения неоднородной
системы.
, и при
различных его значениях мы будем получать различные решения неоднородной
системы.
![]() ,
получаем для общего решения неоднородной системы формулу
,
получаем для общего решения неоднородной системы формулу
![]() .
.